Homogeneously Suslin set
In descriptive set theory, a set  is said to be homogeneously Suslin if it is the projection of a homogeneous tree.
is said to be homogeneously Suslin if it is the projection of a homogeneous tree.  is said to be
is said to be  -homogeneously Suslin if it is the projection of a
-homogeneously Suslin if it is the projection of a  -homogeneous tree.
-homogeneous tree.
If 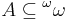 is a
is a 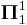 set and
set and  is a measurable cardinal, then
is a measurable cardinal, then  is
is  -homogeneously Suslin. This result is important in the proof that the existence of a measurable cardinal implies that
-homogeneously Suslin. This result is important in the proof that the existence of a measurable cardinal implies that 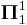 sets are determined.
sets are determined.
See also
References
- Martin, Donald A. and John R. Steel (Jan., 1989). "A Proof of Projective Determinacy". Journal of the American Mathematical Society (American Mathematical Society) 2 (1): 71–125. doi:10.2307/1990913. JSTOR 1990913.